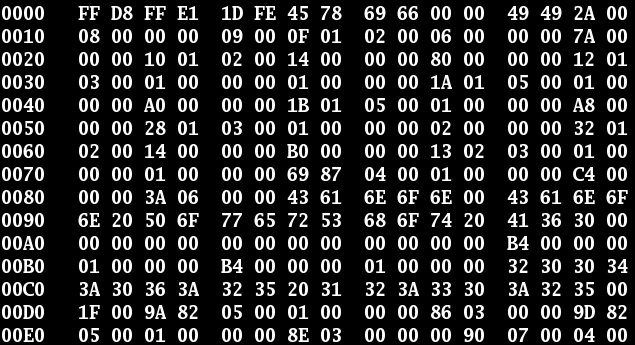
زبان باینری چیست ؟

زبان رایانه ها ، زبان باینری ( Binary ) یا همان صفر و یک است.کوچکترین واحد داده در رایانه بیت نام دارد که می تواند مقدار 0 یا 1 را در خود جای دهد.یعنی هر بیت می تواند 2 حالت متفاوت داشته باشد. از تجمع 8 بیت ، یک بایت تشکیل می شود و مابقی  واحد های داده اعم از کیلوبایت ، مگابایت ، گیگابایت و ... از تجمع تعدادی از بیت ها تشکیل می شود. به نسبت تعداد بیت های استفاده شده در واحد های بزرگتر،حالت های قابل اجرا تغییر می کند و هرچه تعداد بیت ها بیشتر باشد،حالت های بیشتری برای اجرا وجود دارد.

این حالت ها در واقع همان دستورات زبان باینری هستند.در زبان باینری فقط دو عدد 0 و 1 وجود دارد . یعنی فقط حالت روشن یا خاموش وجود دارد و این امر باعث افزایش سرعت پردازش در رایانه ها می شود. اما اگر قرار بود از اعداد بر مبنای 10 ( یعنی اعداد 0 تا 9 ) استفاده  کنیم ،حالت ها افزایش  پیدا می کرد و پردازش اطلاعات سخت تر می شد و مسلما  سرعت کاهش پیدا  می کرد.پردازش دودویی برای رایانه ها راحت تر است ،همچنین فضای کمتری را نیز اشغال می کند.

محاسبه ی اعداد بر مبنای دو

اعدادی که ما در زندگی روزمره و واقعی از آنها استفاده می کنیم،اعداد بر مبنای 10 هستند.اصلا منظور از مبنای 10 چیست و چه تفاوتی با مبنای 2 دارد؟

همانطور که در تصویر مشخص است،راست ترین رقم در اعداد بر مبنای 10 ارزشی معادل  010  دارد. رقم سمت چپ آن1 10 و به همین ترتیب هرچه به سمت چپ می رویم به ارزش ها افزوده می شود.در اعداد بر مبنای 2 یا همان دودویی اعداد به جای 10 بر مبنای 2 محاسبه می شوند.ضمن اینکه ارقام تشکیل دهنده ی  این اعداد فقط 0 و 1 هستند. به تصویر بعدی دقت کنید

در محاسبه اعداد بر مبنای2 هم دقیقا مانند مبنای 10 رفتار می شود بااین تفاوت که راست ترین رقم ارزشی معادل 02 دارد،سمت چپ آن ارزش 12 دارد و هرچه به سمت چپ می رویم ارزش ارقام افزایش پیدا می کند.

نحوه نمایش متن به زبان باینری

به جدول زیر دقت کنید

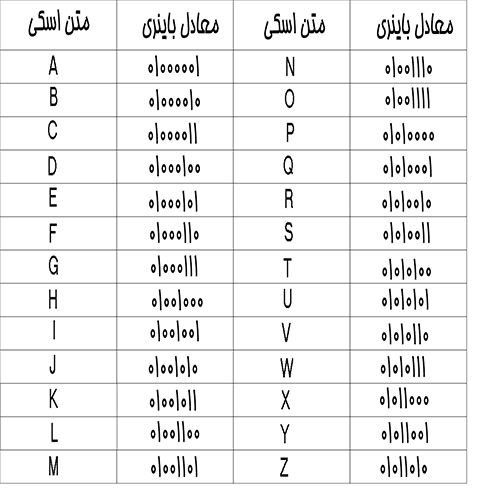
برای ساخت یک کلمه کافیست کدهای حروف آن کنار هم چیده شوند. به مثال زیر توجه کنید : 

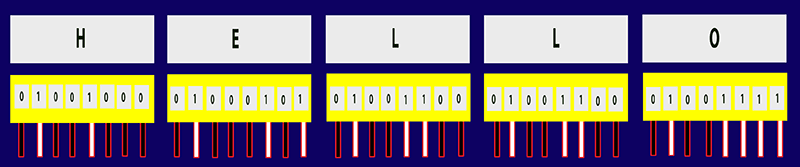
در این تصویر خطوط سفید و مشکی نشان دهنده ی سیگنال های  خاموش  یا روشن هستند که ترکیب آنها یک کد باینری ایجاد می کند. از کنارهم قرار دادن این کدها می توانیم کلمه،جمله و پاراگراف ایجاد کنیم.

نحوه ی نمایش تصاویر در زبان باینری

تصاویر در رایانه از قسمت های کوچکی به نام پیکسل تشکیل شده اند . تصور کنید یک پازل دارید  که هر قطعه تنها یک رنگ دارد از کنارهم قرار دادن  قطعات مختلف پازل تصویر کاملی تشکیل می شود.

نحوه ی نمایش رنگ ها در زبان باینری

همانطور که رنگ ها در دنیای واقعی از ترکیب سه رنگ اصلی قرمز،سبز،آبی تشکیل شده است در رایانه ها هم رنگ ها به همین صورت ایجاد می شوند.تمامی صفحه نمایش ها یا مانیتور ها از تعداد زیادی پیکسل تشکیل شده اند، این پیکسل ها با پیکسل تصاویر متفاوت است.به پیکسل های مانیتور، پیکسل های سخت افزاری و به پیکسل تصاویر،پیکسل های نرم افزاری می گویند.هرچه میزان پیکسل های مانیتور بیشتر باشد وضوح تصویر نیز بالاتر است. هر پیکسل در مانیتور  از سه رنگ قرمز،سبز،آبی  تشکیل شده  که با تغییر غلظت هرکدام از این سه رنگ، یک رنگ جدید ایجاد می شود

در  سیستم های کامپیوتری،مانیتور ها و صفحه نمایش ها هر تصویر یا ویدئو حدودا شامل 16 میلیون رنگ است.یکی از روش های کد گذاری رنگ RGB نام دارد که سه مقدار برای رنگ های قرمز،سبز و آبی دریافت می کند. هر کدام از این سه رنگ می توانند مقداری بین 0 تا 255 را داشته باشند. با تغییر بازه ی عددی رنگ ها نیز تغییر می کنند. به تصاویر زیر دقت کنید :

هرکدام از ردیف ها در تصویر قبل سه باکس با کد رنگ متفاوت دارند. در صورتیکه رنگ پایه ی هر ردیف یکسان است.

نمایش ویدئو ها در کامپیوتر دقیقا مانند تصویر است. زیرا ویدئو از هزاران تصویر تشکیل شده و هر تصویر نیز شامل هزاران پیکسل است که یک کد رنگ خاص دارند.

چرا رایانه ها از سیستم باینری استفاده می کنند؟

دلیل اصلی این است که هر عدد در رایانه به صورت یک سیگنال الکتریکی است. در گذشته اندازه گیری این سیگنال ها بسیار دشوار بود. راه ساده برای اندازه گیری سیگنال ها این است که تنها دو حالت  امکان  داشته باشد،یعنی روشن یا خاموش.تصور کنید دو حالت دیگر مثلا کمی روشن یا کمی خاموش هم جز حالات سیگنال ها بود !! چطور می توانستیم از سیگنال ها برای محاسبات یا ذخیره  یا پردازش استفاده کنیم. مسلما کار بسیار دشوار بود.اما این امر به این معنی نیست که امکان ساخت چنین رایانه هایی وجود ندارد.اما به دلیل سازگاری دنیای امروز با این سیستم عددی در رایانه ها ، هماهنگی مجدد تکنولوژی ها با روشی غیر از باینری بسیار زمان بر خواهد بود. فرض کنید میلیون ها میلیون رایانه باید با سیستم عامل ، نرم افزار ها و برنامه های جدید هماهنگ شوند که کاری بسیار زمان بر و دشوار است. اما این امر به معنی غیر قابل انجام بودن نیست.